Both Hazen-Williams and Darcy-Weisbach equations compute head loss due to friction in a pipe. Hazen-Williams coefficient is a function of only the pipe roughness vs Darcy-Weisbach which considers internal roughness, velocity, and hydraulic slope. In this article, you will learn more about the Hazen-Williams and Darcy-Weisbach equations, and compare the use of both with each other as well as other formulas.
Hazen-Williams Equation
The Hazen-Williams equation stems from using empirical methods in predicting head loss in a water pipe when flow is turbulent. Before the advent of more sophisticated models such as Darcy-Weisbach, the use of Hazen-Williams was predominant amongst engineers. Moreover, it predicts frictional head loss (hf) as a function of the pipe length (L), friction coefficient (C), flow rate (gpm), and pipe internal diameter (d).
![]()
The equation above is the expression for the head loss in imperial units. Alternatively, in S.I. units, the symbol for flow rate (Q) changes with the expression as follows:
![]()
Due to limiting effects from the friction coefficient (C) the Hazen-Williams approach is simply an approximation of losses. The coefficient does not account for viscosity changes and is valid for fluids with a kinematic viscosity of around 1.13 centistokes. As a result, it is accurate for only water around room temperature. In addition, it does not consider the effects of Reynolds number and is valid for flow speeds less than 10 feet/s and pipe diameters greater than 2 inches.
Nevertheless, the use of this equation is still common in sprinkler systems and water supply networks. When combined with the appropriate friction coefficient for the pipe material, satisfactory results may be achieved. Beyond these applications, the Darcy-Weisbach equation is preferable to the Hazen-Williams equation.
Darcy-Weisbach Equation
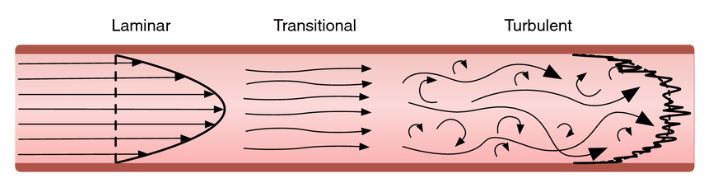
The Darcy-Weisbach equation uses a more accurate friction coefficient vs Hazen-Williams as it comes from the Moody diagram. This diagram incorporates Reynold’s numbers, thus offering a more robust equation across wider range of viscosity, flow speed, and pipe diameter sizes. Darcy-Weisbach predicts head loss (Δhf) as a function of the pipe length (L), mean flow velocity (u), friction factor (f), gravity acceleration (g), and flow diameter (D).
![]()
This equation provides accurate results for steady state and incompressible flow. Also, the Darcy-Weisbach friction factor depends on the Reynolds number and the pipe roughness, as specified from the Moody diagram. Some Moody charts specify an alternative, which is the Fanning friction factor (Cf).
![]()
Both friction factors carry identical information, but the Fanning factor is a quarter of the Darcy-Weisbach factor. So, it is necessary to find out which one a Moody chart specifies prior to use.
The Use of Hazen-Williams vs Darcy-Weisbach
The Darcy-Weisbach equation is an improvement on the Hazen-Williams with several differences as the table below shows.
| Hazen-Williams | Darcy-Weisbach |
| Its friction factor/coefficient considers only the pipe material. So, it accurate for a specific range of viscosity, flow speed, and diameter. | The friction factor considers the effect of Reynold’s number and pipe roughness. Thus, it is more robust and gives accurate results for a variety of flows. |
| The use of this equation is limited to irrigation and water distribution systems. | Darcy-Weisbach equation is suitable for all steady-state, incompressible flow systems. |
| Offers a quick and simplified way of approximating frictional losses in flow systems. | Several considerations make using this equation complicated and time-consuming. |
| Has the option of only one friction factor that relates to the pipe internal roughness. | Could use either Fanning or Darcy-Weisbach friction factor. Although they have the same meaning. |
Hazen-Williams vs Darcy-Weisbach vs Others
Apart from Hazen-Williams and Darcy-Weisbach equations, there are others that serve in estimating head/pressure loss in flow systems. The following sections highlight their differences from these popular approaches.
Hazen-Williams vs Manning
Manning equation provides a versatile formula that is popular in computing several parameters about water resources. Unlike Hazen-Williams vs Darcy-Weisbach, the Manning equation computes flow in open channels. In addition, it can derive the capacity of a pipe, check the performance of an area-velocity flow meter, and compute friction losses. The basic form of the Manning equation relates the flow rate (Q), Manning’s roughness coefficient (n), hydraulic radius (Rh), channel slope (S), and a unit conversion factor (k).
![]()
For S.I. units, the unit conversion factor has a value of 1, but when using imperial units the value is 1.49. Moreover, the hydraulic radius is a ratio of the flow cross-sectional area (A) to the wetted perimeter of the channel (P). This variable accounts for the channel geometry and gives the equation the flexibility of dealing with diverse geometries for the flow channel. Computing the head loss from Manning is simply a product of the channel slope (S) and the channel length (L).
![]()
Although both the Manning and Hazen-Williams equations are for calculating the flow of water, there are fundamental differences, which the following table highlights.
| Hazen-Williams | Manning |
| Used for pipelines with full flow or pressurized flow. | Serves for open channels or pipelines with a partial flow such as sewer lines. |
| Simpler to use, but the error is large when pipe roughness increases and flow parameters exceed certain ranges. | Provides more accurate results in rougher flow channels. |
| The friction coefficient is a factor of only the surface roughness of the flow path. | Manning coefficient varies with surface roughness and the nature of flow path or sinuosity. |
Hazen-Williams vs Colebrook-White
The Colebrook-White equation is ideal for calculating the Darcy-Weisbach friction coefficient in turbulent flows that exceed Re = 4,000. It expresses this friction factor (f), as a function of the hydraulic diameter (Dh), Reynold’s number (Re), and absolute pipe roughness (e).
![]()
Because the friction factor is on both sides of the equation it requires iterative computation. Before the computer era, achieving this was difficult. But now, this equation enjoys adoption for a variety of fluids. The table below highlights some of its differences in relation to the Hazen-Williams equation.
| Hazen-Williams | Colebrook-White |
| Offers a simple approach to determine friction factor. | The equation is implicit, so requires several iterations to solve. |
| The friction coefficient does not consider Reynold’s number effect. | Unlike Hazen-Williams, its friction coefficient accounts for Reynold’s number, and is identical to that of Darcy-Weisbach. |
| It is useful for only water flow. | Its application cuts across both gas and liquid pipelines. |
Darcy-Weisbach vs Manning
The Darcy-Weisbach and Manning equations are both useful in estimating head loss. They have differences, which the following table highlights.
| Darcy-Weisbach | Manning |
| This can serve for calculations for a variety of fluid flows. | It serves only water flow. |
| Provides accurate results for both partial and pressurized flows. | Only accurate in partial or open channel flow. |
| The Darcy-Weisbach coefficient encapsulates the effects of Reynolds number and channel roughness. | Manning coefficient is a function of channel roughness and sinuosity. |
Darcy-Weisbach vs Colebrook-White
Both Darcy-Weisbach and Colebrook White are useful for flow calculations in a variety of fluids. Also, they utilize the same friction factor. However, there are differences between them, which the table below outlines.
| Darcy-Weisbach | Colebrook-White |
| Mostly for steady state, pressurized flow, although adjustments to flow diameter enable it to serve for open channels. | Serves for both open channel and pressurized flow. |
| Accurate for both transition and fully developed turbulent flow. | Accurate in only fully developed turbulent flow with Reynold’s number more than 4,000. |
| Although the Darcy-Weisbach is more complex to solve vs Hazen-Williams, it does not require rigorous computing. | It is an implicit equation that requires several iterations to solve. As a result, it is mostly used on computers. |