Damping Coefficient - Calculation, Values, FAQ

David
Etukudo

Damping coefficient is a material property that measures the ability to absorb energy from a system after loading. For example, a basketball has a low coefficient because it bounces back, rather than absorbing energy. Rubber has a high coefficient and thus aborbs shock impact. Hence, this is why rubber is used in the sole of boots and tires. In this article, we will review how to calculate damping coefficient, its value for certain materials, and commonly asked questions.

Mass-spring system showing damping coefficient — Courtesy: Elprocus

How to Calculate Damping Coefficient

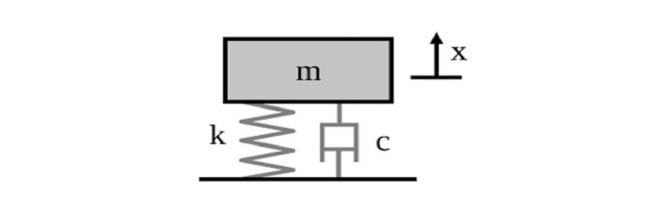
Damping varies according to the type of material, and for an oscillating system, it depends on other physical attributes. For example, in a mass-spring system, there are two common ways of expressing the critical damping coefficient (c_c). First is a function of the spring stiffness (k) and the mass (m) of the oscillating object.

$c_{c}=2\sqrt{k\times m}$

The other way to express c_c relates the mass and the object’s natural frequency (ω_n).

$c_{c}=2m\times \omega _{n}$

Either way, these expressions calculate the critical damping coefficient, which is the value in an ideal scenario. At this critical value, the system moves quickly to attain equilibrium after a disturbance without oscillating. Although engineers try to achieve critical damping in all systems to avoid excessive vibrations, a system can also be overdamped or underdamped.

Overdamping is when the coefficient is greater than the critical value. As a result, there will be a slow return to equilibrium without oscillation. This is not desirable because subsequent disturbances to the system takes it further away from equilibrium, which could be dangerous. On the other hand, underdamping refers to when the coefficient is less than the critical value. It results in a quick return to equilibrium but with oscillations.

Damping Coefficient Units

The S.I. units for damping coefficient are Ns/m. Obtaining this is possible by a dimensional analysis of any of the two equations for calculating the coefficient. For example, using the first equation from the previous section, its units can be derived as follows:

$\sqrt{k\times m}=\sqrt{\left ( \frac{N}{m} \right )\times kg}=\sqrt{\left ( \frac{kg\times m}{s^{2}\times m}\times kg \right )}=\sqrt{\frac{kg^{2}}{s^{2}}}=\frac{kg}{s}$

The units kg/s appear to be different from the S.I. units Ns/m, but a reduction of this S.I. units shows that they are fundamentally the same.

$\frac{N\times s}{m}=\frac{kg\times \frac{m}{s^{2}}\times s}{m}=\frac{kg}{s}$

Damping Coefficient of Materials

The actual damping coefficient for a material varies with stress amplitude, load distribution, geometry, alongside other factors. Because of these multiple variables, determining the actual damping value is difficult using theory. So, estimation often requires an empirical process. This has been done for common materials as the table below shows.

System	Viscous Damping Ratio (ξ)
Auto shock absorbers	0.3
Rubber	0.05
Reinforced concrete structures	0.04 to 0.07
Prestressed concrete structures	0.02 to 0.05
Small diameter piping systems	0.01 to 0.02
Large diameter piping systems	0.02 to 0.03
Metals (operating within elastic region)	Less than 0.01
Continuous metal structures	0.02 to 0.04
Metal structures with joints	0.04 to 0.07

Damping Ratio of Common Engineering Materials

In practice, it is common to quote the damping ratio rather than the actual damping coefficient. This value is a ratio of the materials actual coefficient (c) to the critical coefficient (c_c).

$\xi =\frac{c}{c_{c}}$

From the damping figures on the table, it is clear to see why most engineering structures require the use of certain materials to improve their damping.

Commonly Asked Questions

This section reviews common questions about the concept of the damping coefficient.

What does the damping coefficient depend on?

The damping coefficient of a system depends on the damping of materials that make up the system, and the friction at its connections. As for the damping of each material, it depends on a host of factors including:

Stress amplitude.
Load distribution.
Geometry.
Temperature.
Quality of surfaces.
Number of loading cycles.

What is the damping coefficient in SHM?

Taking the example of a mass-spring system, Newton’s second law motion equation is

$ma+cv+kx=0$

$m\frac{d^{2}x}{dt^{2}}+c\frac{dx}{dt}+kx=0$

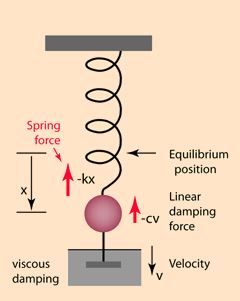
Mass-spring system showing forces due to spring and damping — Courtesy: Hyperphysics

The second term represents the damping force, which is a product of the damping coefficient (c) and velocity (v). Because the equation is in the form of a homogenous second-order differential equation, it has a solution in the form of:

$x=e^{\lambda t}$

Substituting this gives an auxiliary equation for λ.

$m\lambda ^{2}+c\lambda +k$

With the roots of the quadratic auxiliary equation as follows:

$\lambda =\frac{-c\pm \sqrt{c^{2}-4mk}}{2m}$

So, for SHM, the three common scenarios are overdamping, critical damping, and underdamping as the respective equations show.

$c^{2}-4mk> 0$

$c^{2}-4mk= 0$

$c^{2}-4mk< 0$

For an ideal SHM with no friction, the damping is zero, meaning that the oscillations will continue indefinitely.

How is damping measured?

The critical damping coefficient of a system is a function of its mass (m), natural frequency (ω_n), and stiffness (k) as the following equations depict.

$c_{c}=2\sqrt{k\times m}$

$c_{c}=2m\times \omega _{n}$

But measuring the actual damping requires empirical methods that vary depending on the type of system. Some of the methods include Modified Oberst Method, Central Impedance Method, and the Seismic Response Method.

What is a good damping coefficient?

A good damping coefficient is relative and will depend on the application. In industry, the damping ratio is the predominant value in use and refers to the ratio of the actual damping to the critical damping. A damping ratio of 1 is ideal and depicts critical damping. Values less than 1 means underdamping, and values over 1 indicates an overdamped system. Generally, most systems with good damping have values between 0.3 and 0.7.

Damping Coefficient – Calculation, Values, FAQ

Engineering