Engineering stress and true stress are common ways of measuring load application over a cross-sectional area. Moreover, these concepts serve in highlighting the stress-strain relationship in a structure or member from the onset of loading until eventual failure. In this article, we explore the definition of engineering stress and true stress, the stress-strain curve, and their differences in terms of application.
Definition of Concepts
The concepts of engineering stress and true stress provide two different methods of characterizing a material’s mechanical properties. Generally, to determine engineering and true stress values, a sample of material undergoes gradual and documented loading in a tensile test. This provides documentation of its stress-strain relationship until failure.
Definition of True Stress and Strain
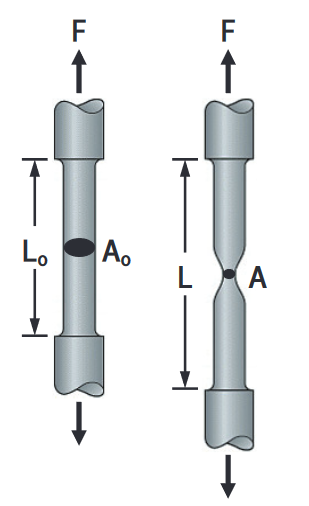
When a sample undergoes loading, its cross-sectional area progressively shrinks before eventual failure. Moreover, as the shrinking progresses, it concentrates on a section, in a process known as necking. So, the true stress represents (σt) the ratio of the instantaneous force on the sample (F) to its instantaneous cross-sectional area (A).
![]()
The true strain (εt) is the natural log of the ratio of the instantaneous length (L) to the original length of the sample (L0).
![]()
In practice, keeping track of this change in area is tedious when analyzing the stress-strain relationship of a test sample. In addition, the true stress-strain does not give insight into the performance of the material when it is in use. Rather, it is ideal for material property analysis by showing the true effect of the strain-hardening behavior and the structure of the sample. Thus, true stress-strain measurement is of more importance to material scientists than engineers.
Definition of Engineering Stress and Strain
On the other hand, the engineering stress (σ) refers to the ratio of the force on a member (F), to its original cross-sectional area (A0).
![]()
While the engineering strain (ε) is the ratio of the change in length (ΔL) to the original (L0) of the sample.
![]()
The engineering stress does not consider the shrinking of the sample, thus, it assumes constant cross-sectional area until failure. The advantage of this approach to analyzing the stress-strain relationship is that it is ideal for calculating most performance-related parameters. For example, values such as toughness, fracture strain, and ultimate tensile strength are easier to evaluate following this approach. Therefore, it is more useful to engineers for designing parts.
Stress-Strain Curve
Stress-strain curves are vital in the fields of engineering and material science. They serve to characterize the material properties of a sample such as ductility, yield strength, and ultimate tensile strength. In addition, engineers use information from them to estimate the Young’s modulus. Generally, to obtain this curve for a material, a sample undergoes a tensile test.
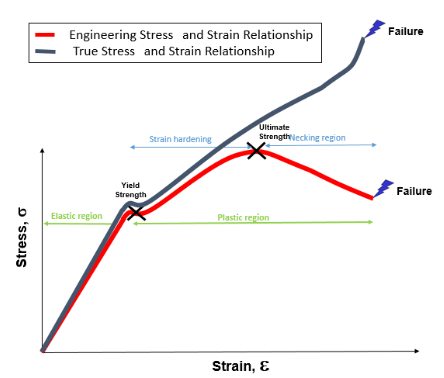
The stress-strain curve above contains both the engineering and true stress-strain relationship. At the onset, the relationship between both curves is fairly the same within the elastic region. But, after yield, the true curve rises until failure. In contrast, the engineering curve rises until the ultimate strength value, then falls until failure.
This is because, in this plastic region, the true curve models strain-hardening much better. As a result, the sample experiences higher stress levels in the plastic region. Also, as necking commences, the true stress rises sharply as it takes into account the reducing cross-sectional area. On the other hand, the ultimate strength indicates the beginning of necking in the engineering curve. Thereafter, the sample can no longer bear more stress as it gets weaker and fails. A review of this curve highlights key differences between the two stress-strain approaches.
Engineering Stress vs True Stress Application
Understanding the differences between the engineering stress-strain and true stress-strain relationship is vital in knowing how to apply them. Furthermore, a review of their stress-strain curve highlights some of these differences.
| Engineering Stress-Strain | True Stress-Strain |
| This relationship is based on the original cross-sectional area of the sample. | This relationship is based on the instantaneous cross-sectional area of the sample as it reduces. |
| Suitable for analyzing material performance, it is used in the design of parts. | It is ideal for material property analysis. |
| It accurately estimates values such as toughness and ultimate strength while hiding the effect of strain-hardening. | It adequately models strain-hardening of the material. However, it obscures ultimate strength. |
| Engineering strain is linear. | True strain is logarithmic. It accurately defines the plastic behavior of ductile materials by considering the actual dimensions. |