Tolerance Analysis – Common Types, in Manufacturing and Product Design

Tolerance analysis entails all processes in determining the variation in size of mechanical parts, and its consequent effects on assemblies. Moreover, this study provides insight into the effects of dimensional variations on assembly functionality, especially in mechanical and electrical systems. In this article, you’ll learn about the types of tolerance analysis and its application in manufacturing and product design.

Types of Tolerance Analysis

There are a variety of approaches to tolerance analysis. However, they are generally categorized into two categories: worst-case analysis and statistical analysis.

Worst-Case Analysis

This is the traditional type of tolerance analysis that guarantees 100% of the parts will assemble and no interference will occur. As the name implies, this model predicts the maximum expected variation of the measurement. Moreover, it involves the direct addition of individual part tolerances to make up the assembly variation. As a result, this method is prone to over-design. For example, there could be an over-exaggeration of the assembly gap as the figure below shows for parts ‘A’, ‘B’, and ‘C’.

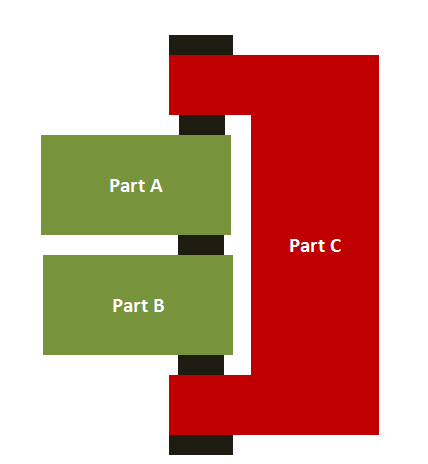
Generally, it is advisable to use this approach for critical applications, in which the allowable parts per million (ppm) defects are zero. Also, this method suits applications with up to three or four parts. A typical worst-case analysis (WCA) follows one direction. Thus, any out-of-plane dimensions result in a need for modifications. For a WCA, the total assembly length (DAsm) is a sum of the lengths of the individual parts. Likewise, the total assembly tolerance (TAsm) is the sum of the tolerance of the individual parts.

   

   

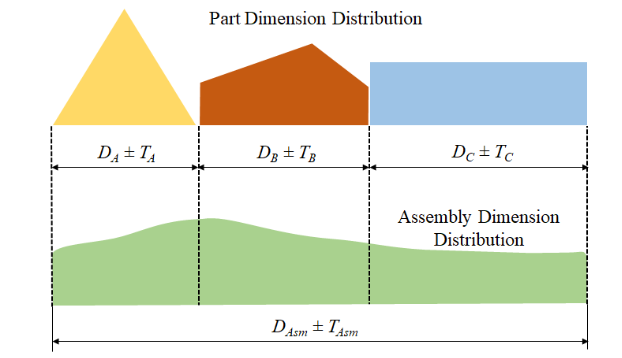
Statistical Analysis

This method applies principles of statistics to relax component tolerances, but without compromising the assembly quality. It requires modelling each component’s variation into a statistical distribution. Then, engineers aggregate these distributions to predict the distribution of the assembly measurement. Thus, it offers a less conservative approach to tolerance analysis than the worst-case analysis. Two common methods of statistical analysis are Root Sum Squared (RSS) analysis and Monte Carlo analysis.

Root Sum Squared Analysis

Unlike in the worst-case analysis, the assembly variation for this method is the root sum square of the individual component tolerance values. This is because of the following assumptions:

• The dimension of each component takes the form of a normal distribution.
• The standard deviation of the dimension is known.

As a result, it is possible to compare the standard deviation of the assembly limits and calculate quality metrics. Such metrics include capability potential, process capability index, and process performance index.

   

   

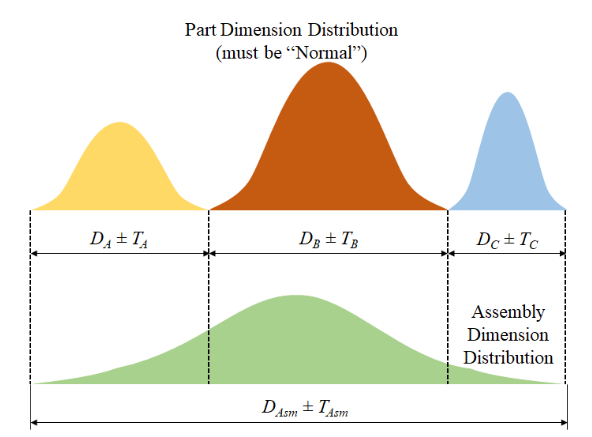
Monte Carlo Analysis

The Monte Carlo analysis is applicable to distributions including and beyond the normal distribution. Moreover, it is an iterative method that calculates assembly variations by randomly changing possible values of each part dimension. Each simulation of this tolerance analysis method involves the random selection of a sample of each part’s dimension.

Then, the random selection calculates interference or clearance. When carrying out these simulations, the percentage of trials that result in an interference fit provides insight into the acceptance rate. Other factors that influence the acceptance rate are the type of distribution of each part and the random number generator.

   

   

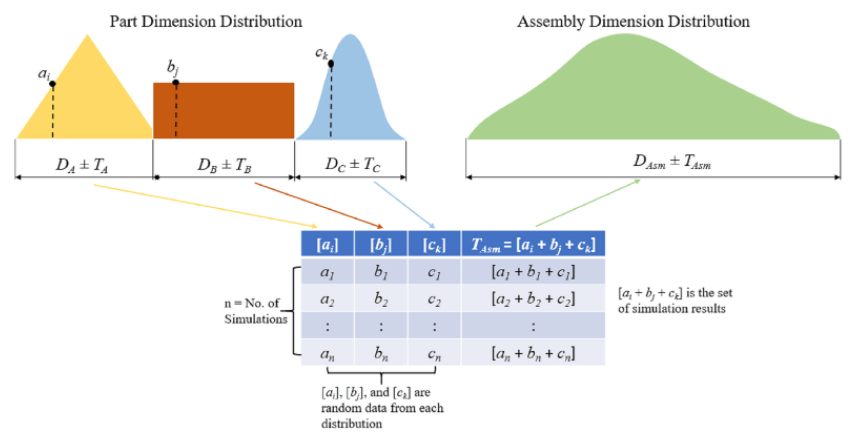
RSS vs Monte Carlo

Both approaches are potent ways of carrying out tolerance analysis. However, RSS provides a more efficient way of handling dimensions with normal distributions. Monte Carlo can serve for dimensions with any other type of probability distribution. Also, Monte Carlo analysis is ideal for assemblies of parts that have non-linear effects on the system.

Tolerance Analysis in Manufacturing and Product Design

As previous sections of this article highlight, tolerance analysis is key to manufacturing and product design. From the design stage, tolerance analysis reveals possible challenges and helps in decision making. The following sections reveal some areas of application of tolerance analysis in industry.

Manufacturing

Because of variations in material characteristics and manufacturing processes, parts are never according to perfect specifications. So, tolerance analysis serves to determine upper and lower acceptable limits on parts dimensions. Subsequently, these limits determine the acceptance rate. In addition, information from this analysis helps to select the appropriate manufacturing method and material for a part, so that it meets specifications.

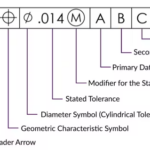
Another aspect of tolerance analysis in manufacturing is enabling communication between clients, engineers, and suppliers. Standards such as ASME Y14.5 establish a uniform practice for stating and interpreting geometric dimensioning and tolerancing. It also provides related requirements, especially for use in engineering drawings and similar documentation.

Product Design

In product design, tolerance analysis has a direct influence on the performance, quality, and cost of a product. Moreover, there is always a compromise between the quality and affordability of products. The tighter the tolerances, the more expensive it is to manufacture.

For example, an aircraft or automobile door may not shut properly if the tolerance is too large. As a result of the poor seal, there will be noise and an impending safety issue with the product. Therefore, using a tighter tolerance, which requires extra cost, makes sense. On the other hand, a product with a short lifecycle, without any safety or functionality concerns, can deploy larger tolerances to save cost.