Generally, the radial force is the force acting perpendicular to the axis of rotation of an object. It acts in a straight line and describes the influence of exertions on an object traveling a circular path. In this article, you will learn more about radial force, how to calculate it, radial force variation, bearing, and testing.
What is Radial Force
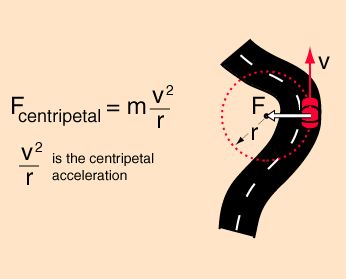
When a body navigates a circular path, there are outward and inward forces acting on it. The outward force is an inertia force (centrifugal), while its inward counterpart is an acceleration force (centripetal force). Both are radial forces and equilibrium between them is what sustains the motion of the body on its path. For example, a car going around a corner experiences a centrifugal force that takes it away from the center of the curve due to its momentum. On the other hand, friction between its tires and road surface acts towards the center to balance the centrifugal force. Thus, it allows the car to navigate the curve smoothly. However, on snowy days where friction is minimal because of ice, cars tend to skid as there is no balance in the radial forces.
Calculation and Formula
In Physics, the representation of force is usually in terms of mass and acceleration, and the radial force is no different. For instance, the radial force (F) on a car maneuvering a curve is a product of its mass (m) and centripetal acceleration. This acceleration is a function of its angular velocity (ω) and the radius of curvature of the road (r). Also, the acceleration can be simply expressed in terms of the vehicle’s linear velocity (v) and the radius of curvature.
![]()
The correlation between the linear and angular velocities is as follows:
![]()
So, the calculation of the radial force is flexible as it could be in terms of either the linear or angular velocity of the body in question.
Radial Force Variation
Radial Force Variation (RFV) is a phenomenon whereby the momentum of a rotating object changes continuously. Moreover, this leads to undesirable vibrations that hinder the performance of equipment such as automobile tires. After manufacturing a tire, measuring the RFV and grading accordingly is a key step for all manufacturers.
Tires with values that are within acceptable limits are put on the cars, while those of poor quality are scrapped. Testing includes measurements for vertical and tangential (fore-aft) tire forces, which are responsible for the vibrations during rotation.
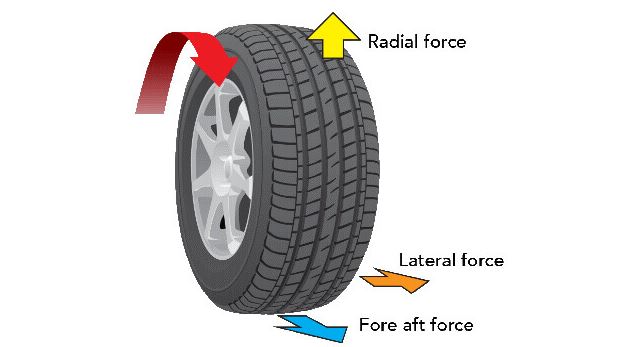
Generally, these forces are due to imperfections in the tire, its assembly, as well as in the smoothness of the road. As a result, there is need for some form of support in the assembly, as well as damping.
Bearing
A wheel bearing is a crucial part of the tire/wheel assembly that connects the wheel to the axle. Although its primary function is to minimize friction in this connection, it also bears the loads coming from the radial force variation. As a result, bearings are subject to internal material stresses leading to wear and eventual failure. So, evaluating the magnitude of these forces and ensuring that the bearings are strong enough to withstand them is necessary.
Radial Force Variation Testing
RFV testing of tires is crucial in the auto industry as it determines the loading and eventual grading of tires. Testing is on the basis that tires are never the same, despite having the same size and manufacturing procedure.
Variations in thickness along the tire and other material defects make them respond differently when rotating. There are two types of testing, according to SAE Practice J332, that manufacturers perform -low-speed and high-speed testing.

Low-Speed Testing
The low-speed test checks for uniformity while loading on a perfectly round rim without tire bead safety humps. It involves rotating the tire at low speeds and taking measurements of variations in radial force after the tire warms. So, a tire with RFV of 20-pounds force indicates that for every rotation, the tire induces an upward force of 20-pounds.
High-Speed Testing
High-speed RFV measurements give a better indication of the variations the vehicle will experience when on highways. Because many tires change shape significantly at high speeds, and exhibit levels of imbalance that are absent at lower speeds. In addition to the vertical radial forces, this test reveals tangential forces from the tire.
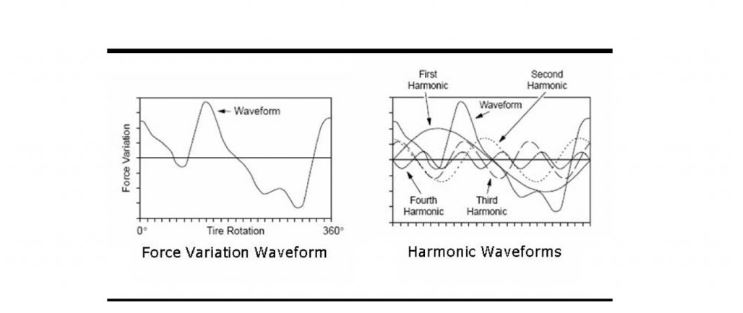
Harmonic Analysis
Another method of characterizing the response of a tire is by analyzing the harmonics of the RFV waveform using Fourier Transform. This enables the parameterization of various aspects of the tire dynamic behavior. Thus, it goes beyond the radial force peaks that the previous methods highlight. Analyzing the harmonics of the RFV waveform reveals more details about the tire response and the causes of the variations.