Etukudo
The cracking of concrete occurs due to several reasons. These reasons include excessive deflection, plastic shrinkage, severe corrosion of steel rebar, etc. However, the concept of cracking moment deals with the cracking of concrete beams due to deflection.
In this article, you will learn the definition of cracking moment, its equation, how to calculate it, and its use pertaining to beams.
Definition
The cracking moment denotes the tensile bending stress at which concrete will start to crack. In practice, concrete excels at withstanding compressive loads but fails under tension. Thus, engineers often use steel to reinforce concrete and improve its tension capacity.
Nevertheless, because the reinforcing steel cross-sectional area is typically 2% or less of the concrete beam cross-section, the beam properties do not change significantly. As a result, they still experience cracking under excessive tensile loads.
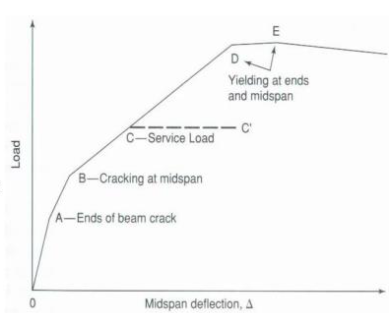
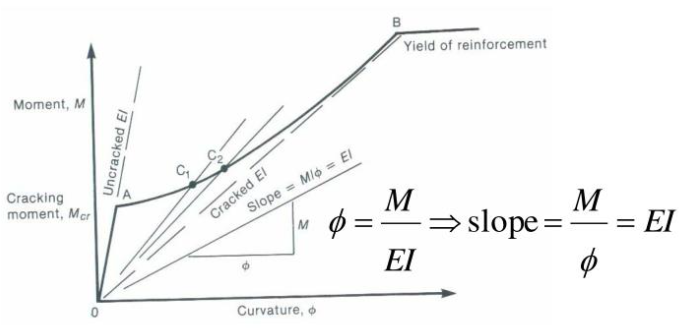
The figures above show the relationship between loading and deflection of a concrete beam. Also, they show how cracking of the beam progresses and affects the beam’s flexural rigidity (EI). Moreover, the onset of cracking (point ‘A’) is typically from the ends of the beam, meaning that this point coincides with the cracking moment.
Cracking Moment Equation
The cracking moment of concrete beam (Mcr) is a function of its gross moment of inertia (Ig), its modulus of rupture (fr), and the distance from its center of gravity (centroid) to the extreme fiber on the tension side of the beam (yt).
![\[ M_{cr}=\frac{f_{r}I_{g}}{y_{t}} \]](https://punchlistzero.com/wp-content/ql-cache/quicklatex.com-601927f54fa95d121545a80bfd44c218_l3.png "Rendered by QuickLaTeX.com")
How to Calculate Cracking Moment
The cracking moment equation shows that the determination of other parameters is a prerequisite to obtaining the moment value. Hence, it is necessary to take a critical look at these parameters, namely the modulus of rupture, momenta of inertia, and distance from the centroid.
Modulus of Rupture
Modulus of rupture refers to the amount of force and compression a beam (usually concrete) can withstand before failure. Moreover, it is a measure of the beam’s resistance to bending, and an important parameter in civil construction parts. For a given concrete beam, the modulus of rupture (fr), is a function of the compression strength of the concrete mix (f’c).
![\[ f_{r}=7.5\sqrt{f_{c}^{'}} \]](https://punchlistzero.com/wp-content/ql-cache/quicklatex.com-cb6d553bb05fc13a6a2978fa73cd2776_l3.png "Rendered by QuickLaTeX.com")
Moment of Inertia
When computing the cracking moment of concrete, convention demands the determination of the gross moment of inertia. For a rectangular cross-section, the gross moment of inertia (Ig), depends on the width (b) and height (h) of the beam.
![\[ I_{g}=\frac{bh^{3}}{12} \]](https://punchlistzero.com/wp-content/ql-cache/quicklatex.com-51b5fd1425d60db60a8afe82fa3b619c_l3.png "Rendered by QuickLaTeX.com")
Another common shape engineers utilize in construction is a circular cross-section. The gross moment of inertia for this shape relates to its radius (r) or diameter (D).
![\[ I_{g}=\frac{\pi r^{4}}{4} or \frac{\pi D^{4}}{64} \]](https://punchlistzero.com/wp-content/ql-cache/quicklatex.com-0f339d0d2423c8fe1badf75a51c54f64_l3.png "Rendered by QuickLaTeX.com")
Distance from Centroid
When a concrete beam deflects under loading, it does so about its center of gravity, or centroid. In addition, the tension along the fibers of the beam varies, with the fiber furthest away from the centroid experiencing the maximum.
As a result, cracking in the concrete commences at the fiber furthest away from the centroid. Thus, its use in the cracking moment formula. For a rectangular cross-section, this distance from the centroid (yt) depends on the height (h).
![\[ y_{t}=\frac{h}{2} \]](https://punchlistzero.com/wp-content/ql-cache/quicklatex.com-4c24a639f537a0de110187c77cd7657e_l3.png "Rendered by QuickLaTeX.com")
The accurate determination of these three parameters (modulus of rupture, moment of inertia, and distance from centroid) is vital in calculating the cracking moment of concrete.
Use of Cracking Moment in Beams
Determining the cracking moment value for concrete serves as a basis for beam design as well as other load-bearing components.
Serviceability
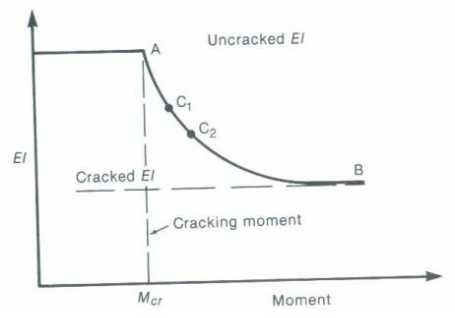
If a concrete beam cracks, its ability to withstand bending (EI) greatly reduces. Subsequently, cracking spreads and failure occurs eventually as loading continues. This relationship between the moment and the flexural rigidity (EI) is vital in construction design. Because from it, engineers can deduce the maximum or allowable deflection of the beam, which coincides with the cracking moment. Furthermore, the formula for obtaining the maximum beam deflection varies depending on the type of beam and load case.
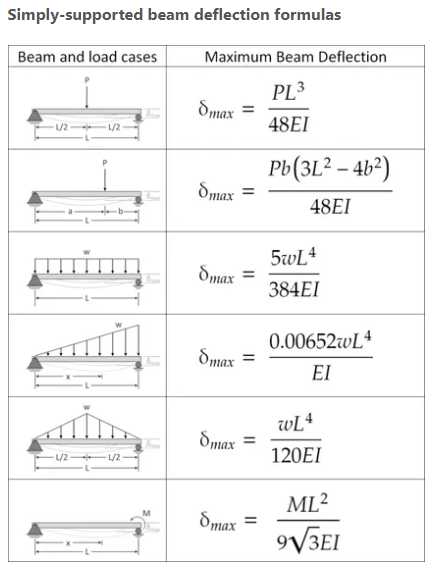
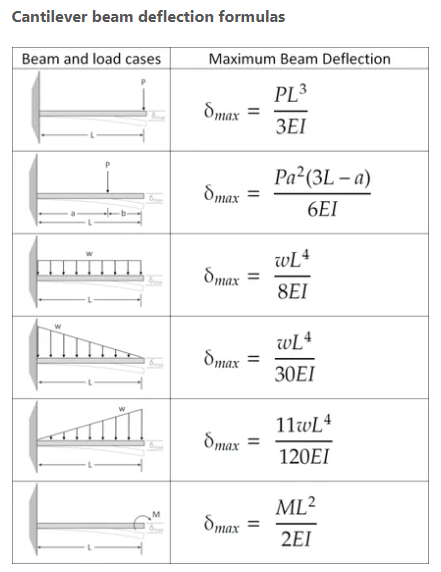
After determining the maximum deflection of a beam before cracking, civil professionals then avoid this loading scenario by using suitable reinforcement spacing and other serviceability measures. Above all, the point of serviceability is to prevent the onset of cracking.
Safety Condition
When a beam or any concrete structure is subject to loading beyond its cracking moment, the next point of call for engineers is to secure the safety of such a member. Now, with the onset of cracking, the objective is to ensure that the section has adequate strength avoid failure.
This is achieved by providing a counter moment that is at least the value of the cracking moment. Codes such as American Concrete Institute (ACI) 318 and European Code (EC2) provide guidance in detail.
