Isentropic is a term that describes a process during which the entropy of the system remains constant. In thermodynamics, isentropic refers to an idealized process, where work transfers of a system are frictionless. As a result, there is no net heat transfer between the system and its environment. In this article, you will learn about the isentropic process, its relationship with thermodynamic laws, isentropic flow, and isentropic vs adiabatic.
Isentropic Process
An isentropic process is an idealization of an actual process. This is due to the assumption that the entropy of the fluid undergoing the process remains constant. Thus, making the process reversible and adiabatic. Obviously, carrying out a constant-entropy process is highly improbable. However, approximating some processes as such is helpful in analyzing thermodynamic systems.
Isentropic Process and the First Law of Thermodynamics
The first law of thermodynamics in terms of enthalpy, equates the enthalpy change (dH) in a process to the sum of heat change (dQ) and work done (Vdp).
![]()
OR
![]()
In this equation, the term Vdp signifies flow process work which is associated with open flow systems such as pumps or turbines. Whereas V is the control volume that does not change, and dp is the change in pressure. For an isentropic process, there is no change in entropy (dS). Thus, the change in enthalpy is equal to the flow process work done on or by the system. Making this assumption allows for easier analysis used in power engineering such as Rankine Cycle and Brayton Cycle.
Isentropic Process and the Second Law of Thermodynamics
According to Clausius statement of the second law of thermodynamics, the change in entropy (dS) of a system, when heat (dQ) is added to it, is related to the temperature at the point of entry (T) as follows:
![]()
This formula is valid only for a reversible process. For an isentropic process, there is no change in entropy; dS = 0. Consequently, there cannot be a transfer of heat energy, meaning the process must be adiabatic; dQ = 0. Therefore, from the second law of thermodynamics, we can infer that a process can only be isentropic if it is reversible and adiabatic.
Isentropic vs Adiabatic
Isentropic and adiabatic are common terms that scientists and engineers use to describe chemical processes that take place in thermodynamic systems. Unfortunately, the misuse of these terms is prevalent due to their similarities. However, there are clear distinctions between an isentropic process and an adiabatic process.
| Isentropic | Adiabatic |
| Isentropic connotes constant entropy. | Adiabatic connotes constant heat energy. |
| For a process to be isentropic, the system must fulfill the following conditions: constant entropy, no heat energy transfer, and reversibility of the process. | For a process to be adiabatic, the only condition is no heat energy transfer between the system and its environment. |
| A process has constant entropy only if it is reversible. | An adiabatic process can be reversible or irreversible. |
| An isentropic process is always adiabatic. | An adiabatic process may or may not be isentropic. |
Constant-Entropy Flow
Isentropic flow is an important concept in the field of fluid dynamics. Furthermore, it refers to a fluid flow with constant entropy, meaning that the flow process is adiabatic and reversible. For this assumption to be valid, then we need to ignore the energy transformations due to friction or dissipative effects during fluid flow. As a result, it is easier to derive several relations to define key parameters of fluid flow such as density, temperature, and pressure.
Constant-Entropy Flow Equations
Approximating a flow to be isentropic is common in practice when a change in flow variables is small and gradual, such as an ideal flow through a nozzle. In addition, the generation of sound waves and a supersonic flow that turns while the flow area increases are both constant-entropy processes.
This approximation enables the derivation of relationships between the temperature (T), volume (V), pressure (P), and density (ρ) of the fluid. We can refer to these as isentropic flow equations for an ideal gas.
![Rendered by QuickLaTeX.com \[ \frac{T_{2}}{T_{1}}=\left (\frac{P_{2}}{P_{1}} \right )^{\frac{\gamma -1}{\gamma }}=\left ( \frac{V_{1}}{V_{2}} \right )^{\gamma -1}=\left ( \frac{\rho _{2}}{\rho _{1}} \right )^{\gamma -1} \]](https://punchlistzero.com/wp-content/ql-cache/quicklatex.com-eb57253de986e01425cd390fbf41200a_l3.png)
In the constant-entropy flow equations above, γ signifies the specific heat ratio of the fluid. For such a flow, if the flow area increases or decreases, it is known as isentropic expansion or isentropic compression respectively.
Isentropic Expansion and Compression
In engineering, constant-entropy expansion and compression of fluids is an assumption with wide usage when analyzing thermodynamic processes.
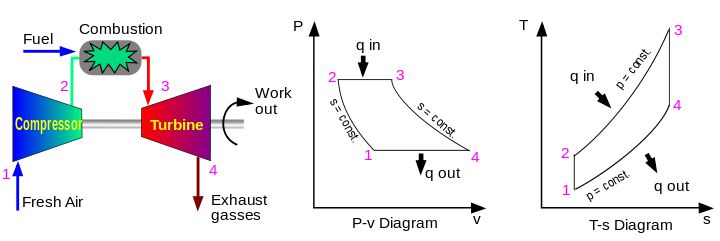
Notably, one area where we use this is in the ideal Brayton cycle. This thermodynamic cycle describes the operations of constant pressure heat engines such as modern gas turbines and airbreathing jet engines. Moreover, the ideal Brayton cycle simplifies the workings of such heat engines into four thermodynamic processes.
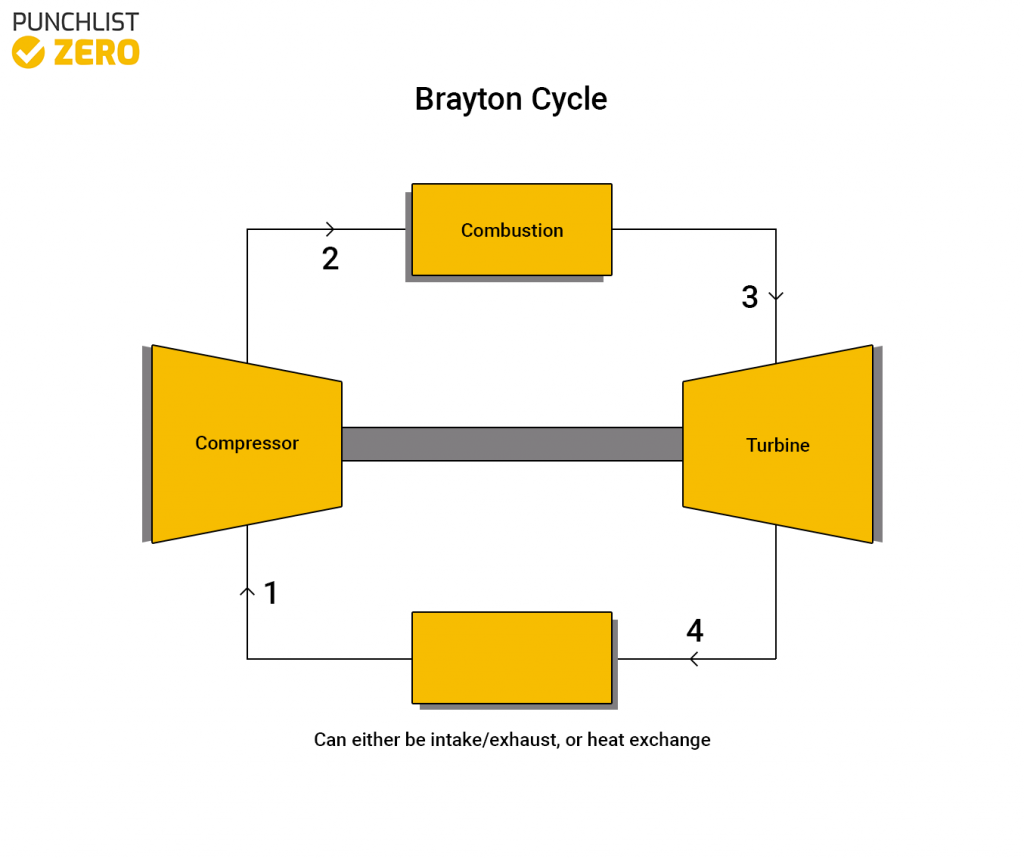
- Isentropic compression (1-2): During this process, the compressor draws in air from the environment and pressurizes it. Thus, making the air ready for use in combustion. Because the entropy of the system is constant during this process, the work done by the compressor (WC) is simply a function of the enthalpy change of the air.
![]()
- Isobaric heat addition (2-3): Next, the compressed air and fuel are mixed and burned in a combustion chamber. This is a constant-pressure process because the chamber remains open to inflow and outflow. Therefore, the net heat added (Qadd) is a function of the enthalpy change.
![]()
- Isentropic expansion (3-4): Subsequently, the heated air gives up its energy as it passes through and turns a turbine or series of turbines. As a result, the air expands, and work is done on the turbine. This is an constant-entropy process, with the work done by the turbine (WT) given as:
![]()
- Isobaric heat rejection (4-1): Finally, the residual heat, which was not used to produce work during isentropic expansion, is rejected to the environment to close the cycle. The net rejected heat (Qrej) is given by:
![]()